As in the basic sampling model, suppose that we select \(n\) numbers at random, with replacement, from the population \(D =\{1, 2, \ldots, m\}\), where \(m, \, n \in \N_+\). Thus, our outcome vector is \(\bs{X} = (X_1, X_2, \ldots, X_n)\) where \(X_i\) is the \(i\)th number chosen. Recall that our basic modeling assumption is that \(\bs{X}\) is uniformly distributed on the sample space \(S = D^n = \{1, 2, \ldots, m\}^n\)
In this section, we are interested in the number of population values missing from the sample, and the number of (distinct) population values in the sample. The computation of probabilities related to these random variables are generally referred to as birthday problems. Often, we will interpret the sampling experiment as a distribution of \(n\) balls into \(m\) cells; \(X_i\) is the cell number of ball \(i\). In this interpretation, our interest is in the number of empty cells and the number of occupied cells.
For \(i \in D\), let \(Y_i\) denote the number of times that \(i\) occurs in the sample: \[ Y_i = \#\left\{j \in \{1, 2, \ldots, n\}: X_j = i\right\} = \sum_{j=1}^n \bs{1}(X_j = i) \] Then \(\bs{Y} = (Y_1, Y_2, \ldots, Y_m)\) has the multinomial distribution with parameters \(n\) and \((1/m, 1/m, \ldots, 1/m)\): \[\P(Y_1 = y_1, Y_2 = y_2, \ldots, Y_m = y_m) = \binom{n}{y_1, y_2, \ldots, y_n} \frac{1}{m^n}, \quad (y_1, y_2, \ldots, y_m) \in \N^n \text{ with } \sum_{i=1}^m y_i = n \]
This follows immediately from the definition of the multinomial distribution, since \((X_1, X_2, \ldots, X_n)\) is an independent sequence, and \(X_i\) is uniformly distributed on \(\{1, 2, \ldots, m\}\) for each \(i\).
We will now define the main random variables of interest.
Random variables.
Clearly we must have \(U + V = m\) so once we have the probability distribution and moments of one variable, we can easily find them for the other variable. However, we will first solve the simplest version of the birthday problem.
The (simple) birthday problem is to compute the probability of the event \(B_{m,n}\) that there is at least one duplication when a sample of size \(n\) is chosen from a population of size \(m\). In terms of the random variables above,
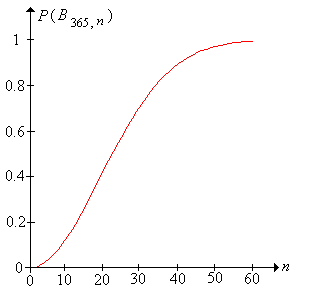
For example, suppose that we choose \(n\) people at random and note their birthdays. If we ignore leap years and assume that birthdays are uniformly distributed throughout the year, then our sampling model applies with \(m = 365\). In this setting, the birthday problem is to compute the probability that at least two people have the same birthday (this special case is the origin of the name). The solution of the birthday problem is an easy exercise in combinatorial probability.
The probability of the birthday event is \[ \P\left(B_{m,n}\right) = 1 - \frac{m^{(n)}}{m^n}, \quad n \le m \] and \(P\left(B_{m,n}\right) = 1\) for \(n \gt m\)
The complementary event \(B^c\) occurs if and only if the outcome vector \(\bs{X}\) forms a permutation of size \(n\) from \(\{1, 2, \ldots, m\}\). The number of permutations is \(m^{(n)}\) and of course the number of samples is \(m^n\).
The fact that the probability is 1 for \(n \gt m\) is sometimes referred to as the pigeonhole principle: if more than \(m\) pigeons are placed into \(m\) holes then at least one hole has 2 or more pigeons. The following result gives a recurrence relation for the probability of distinct sample values and thus gives another way to compute the birthday probability.
Let \(p_{m,n}\) denote the probability of the complementary birthday event \(B^c\), that the sample variables are distinct, with population size \(m\) and sample size \(n\). Then \(p_{m,n}\) satisfies the following recursion relation and initial condition:
Let \(m = 365\) (the standard birthday problem).

In the birthday experiment, set \(n = 365\) and select the indicator variable \(I\). For \(n \in \{10, 20, 30, 40, 50, 60\}\) run the experiment 1000 times each and compare the relative frequencies with the true probabilities.
In spite of its easy solution, the birthday problem is famous because, numerically, the probabilities can be a bit surprising. Note that with a just 60 people, the event is almost certain! With just 23 people, the birthday event is about \( \frac{1}{2} \); specifically \( \P(B_{365,23}) = 0.507 \). Mathematically, the rapid increase in the birthday probability, as \(n\) increases, is due to the fact that \(m^n\) grows much faster than \(m^{(n)}\).
Four fair, standard dice are rolled. Find the probability that the scores are distinct.
\(\frac{5}{18}\)
In the birthday experiment, set \(m = 6\) and select the indicator variable \(I\). Vary \(n\) with the scrollbar and note graphically how the probabilities change. Now with \(n = 4\), run the experiment 1000 times and compare the relative frequency of the event to the corresponding probability.
Five persons are chosen at random.
In the birthday experiment, set \(m = 12\) and select the indicator variable \(I\). Vary \(n\) with the scrollbar and note graphically how the probabilities change. Now with \(n = 5\), run the experiment 1000 times and compare the relative frequency of the event to the corresponding probability.
A fast-food restaurant gives away one of 10 different toys with the purchase of a kid's meal. A family with 5 children buys 5 kid's meals. Find the probability that the 5 toys are different.
\(\frac{189}{625}\)
In the birthday experiment, set \(m = 10\) and select the indicator variable \(I\). Vary \(n\) with the scrollbar and note graphically how the probabilities change. Now with \(n = 5\), run the experiment 1000 times and comparethe relative frequency of the event to the corresponding probability.
Let \(m = 52\). Find the smallest value of \(n\) such that the probability of a duplication is at least \(\frac{1}{2}\).
\(n = 9\)
We now return to the more general problem of finding the distribution of the number of distinct sample values and the distribution of the number of excluded sample values.
The number of samples with exactly \(j\) values excluded is \[ \#\{U = j\} = \binom{m}{j} \sum_{k=0}^{m-j} (-1)^k \binom{m - j}{k}(m - j - k)^n, \quad j \in \{\max\{m-n, 0\}, \ldots, m - 1\} \]
For \(i \in D\), consider the event that \(i\) does not occur in the sample: \(A_i = \{Y_i = 0\}\). Now let \(K \subseteq D\) with \(\#(K) = k\). Using the multiplication rule of combinatorics, it is easy to count the number of samples that do not contain any elements of \(K\): \[ \#\left(\bigcap_{i \in K} A_i\right) = (m - k)^n \] Now the inclusion-exclusion rule of combinatorics can be used to count the number samples that are missing at least one population value: \[ \#\left(\bigcup_{i=1}^m A_i\right) = \sum_{k=1}^m (-1)^{k-1} \binom{m}{k}(m - k)^n \] Once we have this, we can use De Morgan's law to count the number samples that contain all population values: \[ \#\left(\bigcap_{i=1}^m A_i^c\right) = \sum_{k=0}^m (-1)^k \binom{m}{k} (m - k)^n \] Now we can use a two-step procedure to generate all samples that exclude exactly \(j\) population values: First, choose the \(j\) values that are to be excluded. The number of ways to perform this step is \(\binom{m}{j}\). Next select a sample of size \(n\) from the remaining population values so that none are excluded. The number of ways to perform this step is the result in the last displayed equation, but with \(m - j\) replacing \(m\). The multiplication principle of combinatorics gives the result.
The distributions of the number of excluded values and the number of distinct values are now easy.
The probability density function of \(U\) is given by \[ \P(U = j) = \binom{m}{j} \sum_{k=0}^{m-j} (-1)^k \binom{m-j}{k}\left(1 - \frac{j + k}{m}\right)^n, \quad j \in \{\max\{m-n,0\}, \ldots, m-1\} \]
The probability density function of the number of distinct values \(V\) is given by \[ \P(V = j) = \binom{m}{j} \sum_{k=0}^j (-1)^k \binom{j}{k} \left(\frac{j - k}{m}\right)^n, \quad j \in \{1, 2, \ldots, \min\{m,n\}\} \]
In the birthday experiment, select the number of distinct sample values. Vary the parameters and note the shape and location of the probability density function. For selected values of the parameters, run the simulation 1000 and compare the relative frequency function to the probability density function.
The distribution of the number of excluded values can also be obtained by a recursion argument.
Let \(f_{m,n}\) denote the probability density function of the number of excluded values \(U\), when the population size is \(m\) and the sample size is \(n\). Then
Now we will find the means and variances. The number of excluded values and the number of distinct values are counting variables and hence can be written as sums of indicator variables. As we have seen in many other models, this representation is frequently the best for computing moments.
For \(j \in \{0, 1, \ldots, m\}\), let \(I_j = \bs{1}(Y_j = 0)\), the indicator variable of the event that \(j\) is not in the sample. Note that the number of population values missing in the sample can be written as the sum of the indicator variables: \[ U = \sum_{j=1}^m I_j \]
For distinct \(i, \, j \in \{1, 2, \ldots, m\}\),
Since each population value is equally likely to be chosen, \(\P(I_j = 1) = (1 - 1 / m)^n\). Thus, parts (a) and (b) follow from standard results for the mean and variance of an indicator variable. Next, \(I_i I_j\) is the indicator variable of the event that \(i\) and \(j\) are both excluded, so \(\P(I_i I_j = 1) = (1 - 2 / m)^n\). Part (c) then follows from the standard formula for covariance.
The expected number of excluded values and the expected number of distinct values are
The variance of the number of exluded values and the variance of the number of distinct values are \[ \var(U) = \var(V) = m (m - 1) \left(1 - \frac{2}{m}\right)^n + m \left(1 - \frac{1}{m}\right)^n - m^2 \left(1 - \frac{1}{m}\right)^{2 n} \]
In the birthday experiment, select the number of distinct sample values. Vary the parameters and note the size and location of the mean \( \pm \) standard-deviation bar. For selected values of the parameters, run the simulation 1000 times and compare the sample mean and variance to the distribution mean and variance.
Suppose that 30 persons are chosen at random. Find each of the following:
In the birthday experiment, set \( m = 365 \) and \( n = 30 \). Run the experiment 1000 times with an update frequency of 10 and compute the relative frequency of the event in part (d) of the last exercise.
Suppose that 10 fair dice are rolled. Find each of the following:
In the birthday experiment, set \(m = 6\) and \(n = 10\). Run the experiment 1000 times and compute the relative frequency of the event in part (d) of the last exercise.
A fast food restaurant gives away one of 10 different toys with the purchase of each kid's meal. A family buys 15 kid's meals. Find each of the following:
In the birthday experiment, set \(m = 10\) and \(n = 15\). Run the experiment 1000 times and compute the relative frequency of the event in part (d).
The lying students problem. Suppose that 3 students, who ride together, miss a mathematics exam. They decide to lie to the instructor by saying that the car had a flat tire. The instructor separates the students and asks each of them which tire was flat. The students, who did not anticipate this, select their answers independently and at random. Find each of the following:
| \(j\) | 1 | 2 | 3 |
|---|---|---|---|
| \(\P(V = j)\) | \(\frac{1}{16}\) | \(\frac{9}{16}\) | \(\frac{6}{16}\) |
The duck hunter problem. Suppose that there are 5 duck hunters, each a perfect shot. A flock of 10 ducks fly over, and each hunter selects one duck at random and shoots. For the number of ducks killed, find each of the following:
| \(j\) | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| \(\P(V = j)\) | \(\frac{1}{10\,000}\) | \(\frac{27}{2000}\) | \(\frac{9}{50}\) | \(\frac{63}{125}\) | \(\frac{189}{625}\) |